This is an introduction of the ICLR 2019 paper Towards Understanding Regularization in Batch Normalization. This was written in Chinese.

浅谈深度学习：归一化中的正则与泛化

Ping Luo, Xinjiang Wang, Wenqi Shao

关键字：正则，泛化，批归一化 (BN)，参数归一化 (WN)，自适配归一化 (SN)，卡尔曼归一化 (KN)。

0. 前言

一个卷积层、一个批归一化层 (BN)、与一个非线性激活函数一起构成了深度卷积神经网络的“原子”结构。自BN提出以来，研究者们一直尝试更深入的理解它。BN的“秘密”从Ioffe等人的原始文章¹中就能找到蛛丝马迹：文中共4处归功于BN的“隐式”正则化能力，从而带来更大的学习率与泛化性能，并把解释这种隐式正则作为未来的研究方向之一。18年Morcos等人²实验验证指出BN可以使得网络对某个参数或者神经元的依赖性降低，从而使网络在噪声存在时有更好的鲁棒性。这个现象更深层地解释了BN。如何将这种"隐式"的正则显示地表达出来也就成了第一章的主题。第二章探讨BN正则化对其泛化能力的影响。

1. BN与正则

本章浅析BN对网络训练与泛化性能所起的作用。BN的随机过程将转化为确定性过程，其“隐式”正则也将被显式的表达出来。

1.1 一个简单例子

我们知道在神经网络中加入适量噪声可以抑制过拟合。因为随机噪声可以防止网络去拟合输出结果高阶的误差，从而导致其泛化能力变弱。假如能够证明BN也可以等效为一种随机噪声，那么其对网络正则与泛化的影响就明了许多。我们可以先看一个简单情况。如果某变量 $x\sim\mathcal N(0,1)$，已知其全局均值和标准差为 $\mu_\mathcal{P}=0$ 和 $\sigma_\mathcal{P}=1$。若使用小批次样本 (minibatch) 统计出来的 $\mu_\mathcal B$ 和 $\sigma_\mathcal B$ 来对 $x$ 做归一化，我们可以分析其引入的误差为 $(\frac{x-\mu_\mathcal B}{\sigma_\mathcal B}-\frac{x-\mu_\mathcal P}{\sigma_\mathcal P})^2$。这里为简便我们使用Monte-Carlo数值方法来演示，一段简单的python代码如下：

import numpy as np
N=10000; M=32
a=np.random.randn(M, N) #随机生成N批长度为M的标准高斯分布的数据
b=(a-np.mean(a, axis=0))/np.std(a, axis=0) #利用批统计量做归一化
print(np.mean((b-a)**2)) #输出平均误差

不难得到其误差约为 $0.046875=\frac{3}{2M}$（分析过程见后文）。这里 $M$ 为批次大小且 $M=32$。显然由于每个批次中样本数量有限，其统计量的误差导致了每个数据点上的噪声。这只是一个极简单的例子，其在神经网络上的分析和对网络泛化误差 (generalization error) 的影响将在下文介绍。

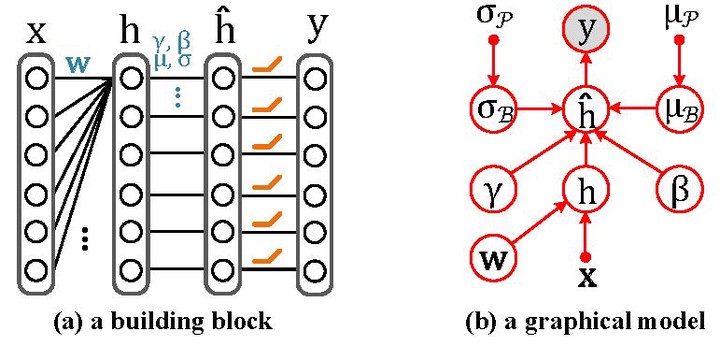
1.2 ConvNet与广义线性模型

如果将多层神经网络看作是嵌套的广义线性模型，我们便可以将其中任意两层单独抽出来分析。为简化计算，我们认为 $\mathbf{x}$ 和 $\mathbf{w}$ 分别代表一小块图像区域 (patch) 和一个卷积核。BN变换之前的特征用 $h=\mathbf{w}^T\mathbf{x}$ 来表示。BN可以写为 $\hat{h}=\gamma\frac{h-\mu_{\mathcal{B}}}{\sigma_{\mathcal{B}}}+\beta$。显然对于每一个小批次而言 $\mu_{\mathcal{B}}$ 和 $\sigma_{\mathcal{B}}$ 是对全局统计量 $\mu_{\mathcal{P}}$ 和 $\sigma_{\mathcal{P}}$ 的近似估计，也就可以视为一个随机量。

假设 $\hat{h}$ 之后的网络可以用广义线性模型 (GLM) 模拟，那网络输出 $y$ 的条件概率分布可以写为 $p(y|\hat{h})=H(y)\exp{y\hat{h}-A(\hat{h})}$，其中 $H(y)$ 以及 $A(\hat{h})$ 分别为 $y$ 和 $\hat{h}$ 的函数。取其负对数似然函数可以得到 $-\log p(y|\hat{h})=A(\hat{h})-y\hat{h}-\log H(y)$。由于最后一项与 $\hat{h}$ 不相关，可以略去。而 $A$ 针对不同的激活函数有不同的形式。这时最大似然的损失函数可以定义为 $\ell(\hat{h})=A(\hat{h})-y\hat{h}$。 假设总的训练数据表示为 $\{\mathbf{x}^{j},y^{j}\}_{j=1}^{P}$ 。则最大似然误差的期望是 $L =\frac{1}{P} \sum_{j=1}^{P}\mathbb{E}_{\mu_{\mathcal{B}},\sigma_{\mathcal{B}}}[\ell(\hat{h}^{j})]$，其中 $\mathbb{E}_{\mu_{\mathcal{B}},\sigma_{\mathcal{B}}}[\cdot]$ 代表损失函数对样本统计量 $\mu_\mathcal{B}$ 和 $\sigma_\mathcal{B}$ 的期望。

1.3 “隐式”正则的形式：PN+Gamma衰减

由于BN的存在，训练过程中对每个样本 $\mathbf{x}^j$ 而言，损失函数不再是一个确定量，而是一个随机量。这是由于 $\mu_{\mathcal{B}}$ 和 $\sigma_{\mathcal{B}}$ 不仅与当前样本相关，还取决于该批次中的其他随机选取的样本。可以认为 $\mu_{\mathcal{B}}$ 和 $\sigma_{\mathcal{B}}$ 满足分布³：$\mu_{\mathcal B} \sim \mathcal{N}(\mu_{\mathcal P}, \frac{\sigma_{\mathcal P}^2}{M})$ 及 $\sigma_{\mathcal B} \sim \mathcal{N}(\sigma_{\mathcal P}, \frac{\rho+2}{4M})$。其中 $M$ 是批次大小，$\rho=\frac{C-\sigma_{\mathcal P}^{4}}{\sigma_{\mathcal P}^{4}}-2$ 代表 $h$ 分布的峰度且有 $C=\mathbb{E}[(\mathbf{w}^{T}\mathbf{x}-\mu_{\mathcal P})^{4}]$。

在网络训练过程中的每个时刻，可以认为全局统计量 $\mu_{\mathcal{P}}$ 和 $\sigma_{\mathcal{P}}$ 可通过全部样本经过本层后统计得出。则 $\ell(\hat{h}^{j})$ 可在 $\ell(\bar{h}^{j})$ 处展开，并且 $\bar{h}^j=\gamma\frac{h^j-\mu_{\mathcal{P}}}{\sigma_{\mathcal{P}}}+\beta$ 可称作全局归一化 (population normalization，PN)。其Taylor展开式可以写作

$$ \ell(\hat{h}^{j}) = \ell(\bar{h}^{j}) + \frac{\partial \ell(\bar{h}^{j})}{\partial \bar{h}^j}(\hat{h}^j-\bar{h}^j)+\frac{1}{2}\frac{\partial^2 \ell(\bar{h}^{j})}{\partial^2 \bar{h}^j}(\hat{h}^j-\bar{h}^j)^2 +\mathcal{O}\big((\hat{h}^j-\bar{h}^j)^2\big) $$

$$=\ell(\bar{h}^{j}) + (A’(\bar{h}^j)-y^j)(\hat{h}^j-\bar{h}^j)+\frac{1}{2}A’'(\bar{h}^j)\cdot(\hat{h}^j-\bar{h}^j)^2 +\mathcal{O}\big((\hat{h}^j-\bar{h}^j)^2\big) $$

以上等式右边的第一项为使用PN代替BN的损失函数，第二项中 $A’(\bar{h}-y)$ 则很容让人联想到广义线性模型中存在 $A’(\bar{h})-\mathbb{E}[y]=0$：在 $P\rightarrow \infty$ 时可以认为 $L=\mathbb{E}_{{\mathbf{x}, y}}{[\ell(\hat{h}^{j}) ]}$，从而可以认为第二项对总损失的贡献可以忽略。第三项的具体形式稍为复杂，但也可根据上述统计量的分布对 $(\hat{h}^j-\bar{h}^j)^2$ 展开后得到⁴。最终形式为

$$ \mathbb{E}_{\mu_{\mathcal{B}},\sigma_{\mathcal{B}}} \big[ (\hat{h}^j-\bar{h}^j)^2 \big]\approx (\frac{\mathbf{w}^T\mathbf{x}-\mu_{\mathcal B}}{\sigma_{\mathcal{B}}})^2\frac{\rho+2}{4M}\gamma^2 + \frac{1}{M}\big(1+\frac{3(\rho+2)}{4M}\big)\gamma^2 $$

其中$\rho$为$\mathbf{w}^T\mathbf{x}$分布的峰度，$M$为批次大小，当$M\rightarrow P$时上述等式成立，在上述推导中一般认为$M>30$。意识到费希尔信息矩阵 (FIM) 即 $F_\gamma^j=\frac{\partial^2 \ell(\bar h^j)}{\partial \gamma^2}={A’'(\bar{h}^j)(\frac{\mathbf{w}^T\mathbf{x}^j-\mu_{\mathcal B}}{\sigma_{\mathcal{B}}})^2}$。因此将上式代入总损失函数 $L$ 后可化简为

$$L\approx \frac{1}{P} \sum_{j=1}^{P} \ell(\bar{h}^{j}) + \zeta(h) \gamma^2,~~~ \zeta(h)=\underbrace{\frac{\rho+2}{8M}F_\gamma}_{\mathrm{from~} \sigma_{\mathcal{B}}}+\underbrace{\frac{\mu_{d^2A}}{2M}}_{\mathrm{from~} \mu_{\mathcal{B}}}. $$

上式中 $\zeta(h)$ 是BN正则项的系数。与一般正则项系数不同，它是关于隐含层 $h$ 的函数，即它的取值与训练数据的前向及反向传播相关。其中 $F_\gamma$ 与 $\mu_{d^2A}$ 分别是FIM和 $A’'(\bar h)$ 在经过全体样本后统计得到的平均值。

综上所述, BN被分解为PN和Gamma衰减 (gamma decay)。我们称此过程做BN的正则化。其中PN利用全局统计量进行归一化操作，它把BN的随机性归一化替换为确定性归一化。Gamma衰减是对 $\gamma$ 的一种数据自适应的二阶正则。由于归一化过程的性质，$\gamma$ 代表该层的缩放系数，也就等价于普通SGD (无BN) 中参数 $\mathbf{w}$ 的模。因此BN的作用也在于约束隐含层的激活。另外 $\zeta(h)$ 中的两项分别来源于 $\mu_\mathcal{B}$ 和 $\sigma_\mathcal{B}$ 的随机性质，体现着不同的作用。同时这两项均与批次大小 $M$ 成反比。也就意味着当批次越大时网络优化过程中BN所赋予的正则效果就越弱。

1.4 特定激活函数的正则形式

以上分析过程并没有针对激活函数以及输入函数的分布作特定假设。而在一些常见的条件下正则项的形式会变得简洁很多。

ReLU函数：此处我们利用连续的SoftPlus函数来替代ReLU函数来逼近 $f(\bar h)=\lim_{t\rightarrow \infty}\frac{1}{t}(1+\exp(t\bar h))$。可以得到 $A’'(\bar h)=f’(\bar h)=\lim_{t\rightarrow\infty}\sigma (t\bar h)=\mathrm{H}(\bar h)$。其中 $\sigma(x) = \frac{1}{1+\exp(-x)}$ 为Sigmoid函数，$H(x)=(\mathrm{sign}(x)+1)/2$ 为Heaviside阶跃函数。所以对于ReLU激活函数，可以得到 $\zeta(h)=\frac{\rho+2}{8M}F_\gamma+\frac{1}{2M}\mathrm{\bar{H} (\bar{h})}$，其中 $\mathrm{\bar{H} (\bar{h})}=\frac{1}{P}\sum_{j=1}^P{\mathrm{\bar{H} (\bar{h}^j)}}$ 代表所有样本的平均被激活值。因此若网络使用ReLU，Gamma衰减可近似为 $\zeta(h)={\frac{\rho+2}{8M}F_\gamma}+{\frac{1}{2M}\frac{1}{P}\sum_{j=1}^P\sigma(\bar{h}^j)}$。

Identity函数：当激活函数为Identity函数 $f(\bar h)=\bar h$ 时，$\zeta(h)$的形式会更加简洁。此时 $\mu_{d^2A}=\frac{1}{P}\sum_{j=1}^P{\bar{h}^j}$。若同时假设全局统计量 ${\bar h}\sim\mathcal{N}(0,1)$，即 $\mu_\mathcal{P}=0$ 和 $\sigma_\mathcal{P}=1$。其损失函数的正则项系数 $\zeta \approx\frac{3}{4M}$，与隐含层取值 $h$ 无关。值得注意的是在做线性回归时一般损失函数定义为 $\ell(\mathbf x)=(\phi(\mathbf x)-y)^2$，所以对其而言 $A’'(\bar h)=2$，因此 $\zeta=\frac{3}{2M}$ (对应文章开头最简单的例子)。另外如果网络中无偏置项则无需统计 $\mu_\mathcal B$。这时 $\mu_\mathcal B$ 对正则项的影响可忽略，得到 $\zeta=\frac{1}{2M}$。

1.5 正则的意义

• 首先，通过BN的正则化过程，BN的“隐式”正则可以显式表示为PN与Gamma衰减。PN使用全局统计量来代替BN中的随机统计量，使训练过程的随机性变为决定性。PN与正则项的搭配让我们可以使用传统方法例如动态系统和统计物理来理解BN的训练过程和泛化能力。 PN与参数归一化 (WN) 有紧密联系。WN的表达式为 $\nu\frac{\mathbf{w}^T \mathbf{x}^j}{\Vert\mathbf{w}\Vert}$。对比其与PN的形式可以看出当输入服从高斯分布且协方差矩阵为以 $a$ 为对角元素的对角阵时 $\bar{h}^j=\gamma\frac{\mathbf{w}^T \mathbf{x}^j-\mu_\mathcal{P}}{\sigma_\mathcal{P}}+\beta=v\frac{\mathbf{w}^T \mathbf{x}^j}{\Vert\mathbf{w}\Vert}+b$，这里 $v=\gamma/a$ 同时 $b=-\frac{\gamma\mu_\mathcal{P}}{a\Vert \mathbf{w}\Vert_2}+\beta$。

• 其次，Gamma衰减的系数 $\zeta(h) = \frac{\rho+2}{8M}F_\gamma + \frac{1}{2M}\mu_{d^2A}$ 包括两项，但它们来源有所不同。第一项 $\frac{\rho+2}{8M}F_\gamma$ 来源于 $\sigma_{\mathcal B}$ 的噪声，其中 $F_\gamma$ 为Hessian矩阵的对角项。由于 $F_\gamma = \mathbb E[(\frac{\partial \ell}{\partial \gamma})^2]$，因此此项等效为——惩罚损失函数反向传播过程中过大的梯度值以及避免在优化中掉入过于陡峭的局部最优点。当考虑多个神经元或多层网络时该项实际减少不同参数之间的相关性 (co-adaptation)，可类比dropout的作用。 而第二项 $\frac{1}{2M}\mu_{d^2A}$ 来源于 $\mu_{\mathcal B}$，且在激活函数为ReLU时形式化为 $\frac{1}{2M}\frac{1}{P}\sum_{j=1}^P\sigma(\bar{h}^j)$。它代表了数据经过本神经元被激活的概率。因此其等效的作用是在一个隐藏层的神经元中惩罚有过大激活值的神经元，从而降低网络输出值对单一神经元的依赖。为此当输入出现一定噪声或者任一神经元被剪枝后对网络的输出不会造成太大影响。

• 另外，值得注意的是本文分析的正则是施加在 $\gamma$ 上的，也就是BN中的缩放系数。但是，在一些软件实现过程中如果BN后面是ReLU，也往往可以不需要这一缩放系数⁵。这样一来BN的正则效果就加在了后面卷积层的核函数上。

2. BN与泛化

2.1 Committee Machine

什么是Committee Machine？得到了BN正则化的具体形式后，我们需要在一些简单的网络中去定量地验证这一形式。一个较为直观的例子便是CommitteeMachine，其最基本形式是一个单层的线性网络。由于其解空间较容易得到，所以在理论分析中广泛地用作定量研究的起点。假设网络输出 $y$ 是由另一具有相同结构但无BN的网络所得到的，$y=\mathbf{w^*}^T\mathbf{x}+\varepsilon$，其中 $\varepsilon\sim \mathcal N(0, \delta^2)$ 是添加在输出上未知的噪声。为简单起见这里把偏置项 $b^*$ 与权重参数 $\mathbf{w^*}$ 合并。这个学习过程也叫做“教师-学生”模型，在此拟合过程中其损失函数为 $L=\frac{1}{P}\sum_{j=1}^{P}(\phi(\mathbf{x}^j)-y^j)^2$，其中 $\phi: \mathbb R^N \rightarrow R$ 为学生网络的函数。它把教师网络的输出 $y$ 作为拟合目标。我们感兴趣的是该拟合过程的“高维”情况，即总样本数 $P$ 和输入 $\mathbf{x}$ 的维度 $N$ 趋于热力学极限 $P\rightarrow\infty$ 和 $N\rightarrow\infty$，但 $\alpha = \frac{P}{N}$ 为一有限值。另外输入 $x^j\sim\mathcal N(0, 1)$，同时教师网络权重的每个元素可满足 $ w^* \sim \mathcal{N}(0, \frac{1}{N})$。因此教师网络的输出即为 $y\sim\mathcal N(0, 1+\delta ^2 )$。

下面我们考察3个不同的学生网络对上述教师网络的噪声强度 $\delta$ 的抑制能力，包括BN，WN+Gamma衰减，与普通SGD（无BN和WN）。

2.2 泛化误差

什么是泛化误差？噪声的抑制能力通常用泛化误差来衡量。由于训练数据是从输入分布中采样得到的，当数据量不足时便会造成过拟合。在这种假设条件下学生网络的泛化误差即为学习过程的损失在输入 $\mathbf{x}$ 下的期望。定义为 $\epsilon_{\mathrm {gen}}(\theta)=\langle[\phi(\mathbf{x})-y]^{2}\rangle_{\mathbf x}$。其中 $\langle\cdot \rangle_\mathbf{x}$ 代表对所有可能的输入 $\mathbf{x}$ 的期望值。针对线性网络上述泛化误差可求得解析解。下面分别针对几种学生网络的解以及它们的泛化能力进行分析。

2.3 解析解与数值解对比

我们将给出WN+Gamma衰减和普通SGD的解析形式，并把它们与BN的数值解进行对比，从而验证BN正则化形式的推导。

SGD网络：普通SGD网络定义为 $\phi(x)=\mathbf{w}^T\mathbf{x}$。此时 $\mathbf{w}$ 收敛的解较易得到，其形式即为Moore-Penrose伪逆解 $\mathbf{w} =\left(\mathbf{x} ^T \mathbf{x} \right)^{+}\mathbf{x} ^T {y}$。对比求解过程中未知数个数 $N$ 和方程个数 $P$，我们不难发现当 $\alpha=P/N<1$ 时其解为欠定，而当 $\alpha>1$ 时其解过定。而当 $\alpha=1$ 时解虽然唯一，但是在极小的扰动 $\varepsilon$ 下得到的解不稳定甚至发散。利用随机矩阵理论我们可以得到 $\Sigma$ 在不同 $\alpha$ 值时的特征值分布，从而得到其泛化误差 $$ \epsilon_{\mathrm{gen}}^{\mathrm{sgd}}=\begin{cases} 1-\alpha+{\alpha\delta^{2}}{/(1-\alpha)}, & \left(\alpha<1\right)\
{\delta^{2}}{/(1-\alpha)}. & \left(\alpha>1\right) \end{cases} $$ 若取 $\delta^2=0.25$ 时其泛化误差随 $\alpha$ 的关系可见下图中蓝线部分。当 $\alpha\in[0,1]$ 以及 $\alpha\gg1$ 时泛化误差随 $\alpha$ 增加而减少，体现在随着训练样本数目增加，模型能更好地学习参数。但是当 $\alpha\approx1$ 时输入的协方差矩阵 $\Sigma=\mathbf{x}^T\mathbf x$ 的特征值在 $0$ 处的分布出现峰值，所以这时其伪逆会极不稳定。也就是说当网络试图去拟合教师网络中的噪声 $\varepsilon$，这时训练会出现很强的过拟合。

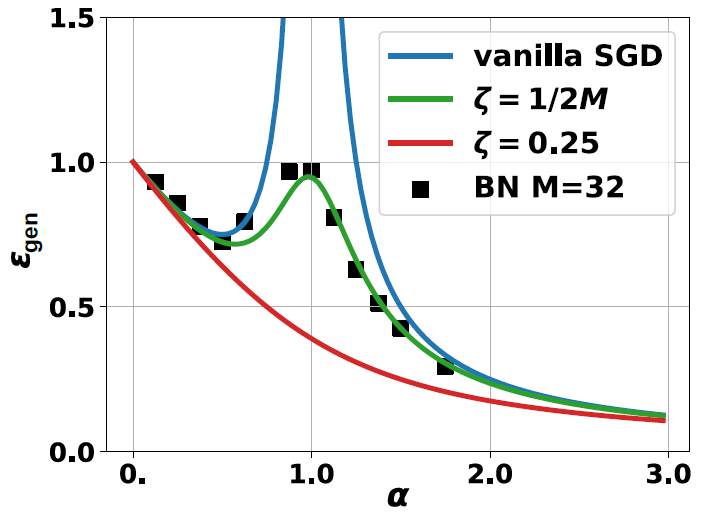
BN网络：BN学生网络的形式为 $\phi(\mathbf{x})=\gamma \frac{\mathbf{w}^T\mathbf{x}-\mu_\mathcal{B}}{\sigma_\mathcal{B}}+\beta$。类似教师网络，我们合并偏置项即 $\beta=0$。在BN的数值实验中我们给定输入维度为 $N=4096$ 以逼近热力学极限 (实际上 $N>100$ 左右已足够)。而 $\alpha$ 的值则依据 $\alpha=P/N$ 中的 $P$ 变化决定。在网络优化过程中我们令批次大小 $M=32$ 以观察BN对网络训练的正则效果。其学习得到的泛化误差在上图中标记为实心方块。其趋势也和普通SGD类似，但这时网络的泛化能力得到了显著的改善。特别地当 $\alpha=1$ 时网络不再发散，因为BN的正则效果使激活 $\gamma$ 不致过大。由前面的分析我们得知BN的引入导致网络对 $\gamma$ 有一个隐含的约束，而当输入满足标准高斯分布时其峰度 $\rho=0$。这时不难算出Gamma衰减的 $\zeta(h)$ 可以简化为 $\zeta=\frac{1}{2M}$ 且与 $h$ 无关。

WN与正则网络：根据上文的分析在当前的设定条件下BN网络可以等价于WN+Gamma衰减。所以我们定义 $\phi(\mathbf x) = \gamma \frac{\mathbf{w}^T\mathbf{x}}{\Vert \mathbf{w}\Vert}+\beta$，同BN一样这里偏置项 $b$ 也合并。与此同时在WN的损失函数 $L$ 后面加上Gamma衰减 $\zeta\Vert \gamma \Vert_2^2$。这里的 $\zeta$ 可以任意取值。例如取 $\zeta=0.25$ 时泛化误差曲线效果最好如上图红线，此时刚好抵消教师网络中的噪声。

不过为了和BN的数值解作比较，我们选取 $\zeta$ 的值由分析BN中得到的等效 $\zeta$ 值来替代。上文已得到在线性网络时 $\zeta=\frac{1}{2M}$。因此我们可以计算出此时的理论泛化误差为 $\varepsilon_\mathrm{gen}^{\mathrm{wn}} = \delta^2\frac{\partial(\zeta G)}{\partial \zeta}-\zeta^2 \frac{\partial G}{\partial\zeta}$，这里 $G=\frac{1-\alpha-\zeta+\sqrt{(\zeta+(1+\sqrt \alpha)^2(\zeta+(1-\alpha)^2))}}{2\zeta}$ 且 $\alpha=P/N$。在上图中，我们将 “$\zeta=\frac{1}{2M}$” 得到的理论 $\varepsilon_\mathrm{gen}^{\mathrm{wn}}$ 值曲线与图中离散的BN数值解结果作对比可以发现二者吻合。由此证明我们得以在数值上验证BN正则化的解析形式。

2.4 CNN中的正则效果

上文在简单的网络中验证了BN的正则化形式。然而实际任务多使用卷积神经网络 (CNN)，它为我们带来更复杂的分析。因此我们首先从实验上去验证。为验证上述正则化效果在具体任务中的表现，我们在同一CNN结构上改变不同的归一化方法进行训练和测试。该CNN由4个卷积层和2个全连接层组成，表述为 “conv(3,32)-conv(3,32)-conv(3,64)-conv(3,64)-pool(2,2)-fc(512)-fc(10)”。其中conv(3,32)表示32个卷积核大小为3的卷积核，pool(2,2)表示一层核大小与步长均为2的池化层，fc(512)表示输出维度为512的全连接层。训练样本我们采用标准CIFAR-10数据。所有网络训练过程均未使用数据增强和参数衰减 (weight decay) 以突出BN的正则效果。

2.4.1 PN+Gamma衰减与BN等效？

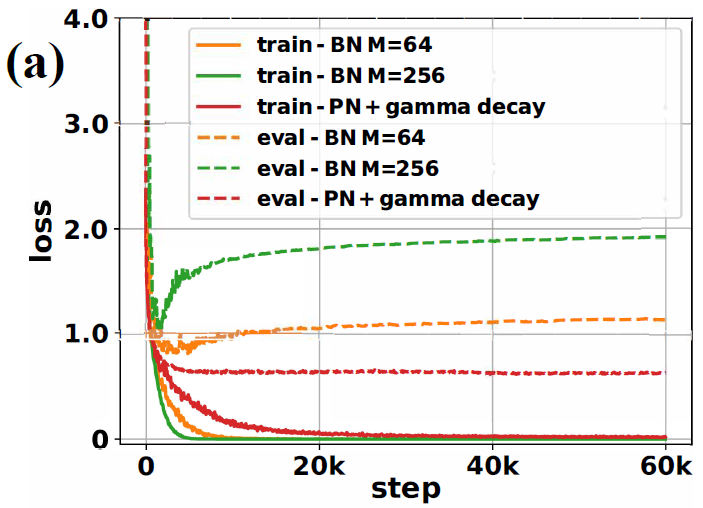
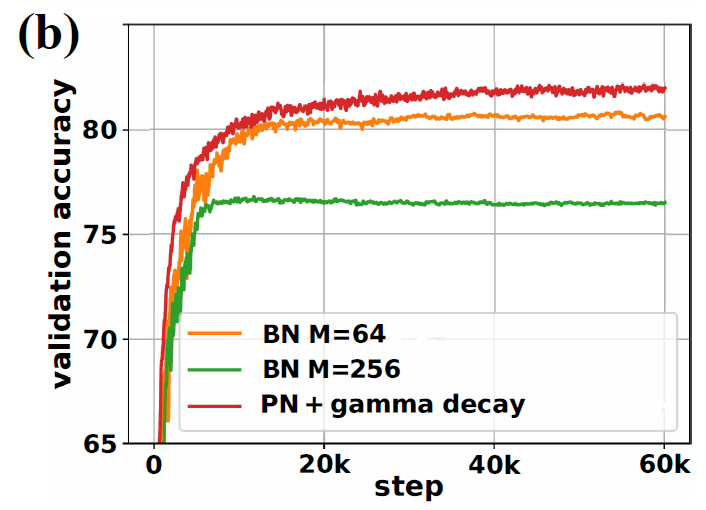
我们将验证在CNN中PN+Gamma衰减能否等效于BN。这里使用 $M=64$ 来训练BN。下图可观察 $M$ 从64增加到256时泛化能力减弱。对于PN我们需要估计全局统计量与 $\zeta(h)$ 中的两项 $F_\gamma$ 和 $\mu_{d^2A}$ 。在CNN中若使用ReLU作为激活函数，$F_\gamma$ 可近似为FIM的condition number，而 $\mu_{d^2A}$ 代表神经元被激活的概率。它们都使用足够多的训练样本来估算 (~10k)。下图显示PN与Gamma衰减能够获得比BN更好的泛化性能。而在实践中类似PN的操作已得到应用例如switchable normalization使用batch average取代moving average。

2.4.2 $\mu_\mathcal{B},\sigma_\mathcal{B}$的正则能力不同？

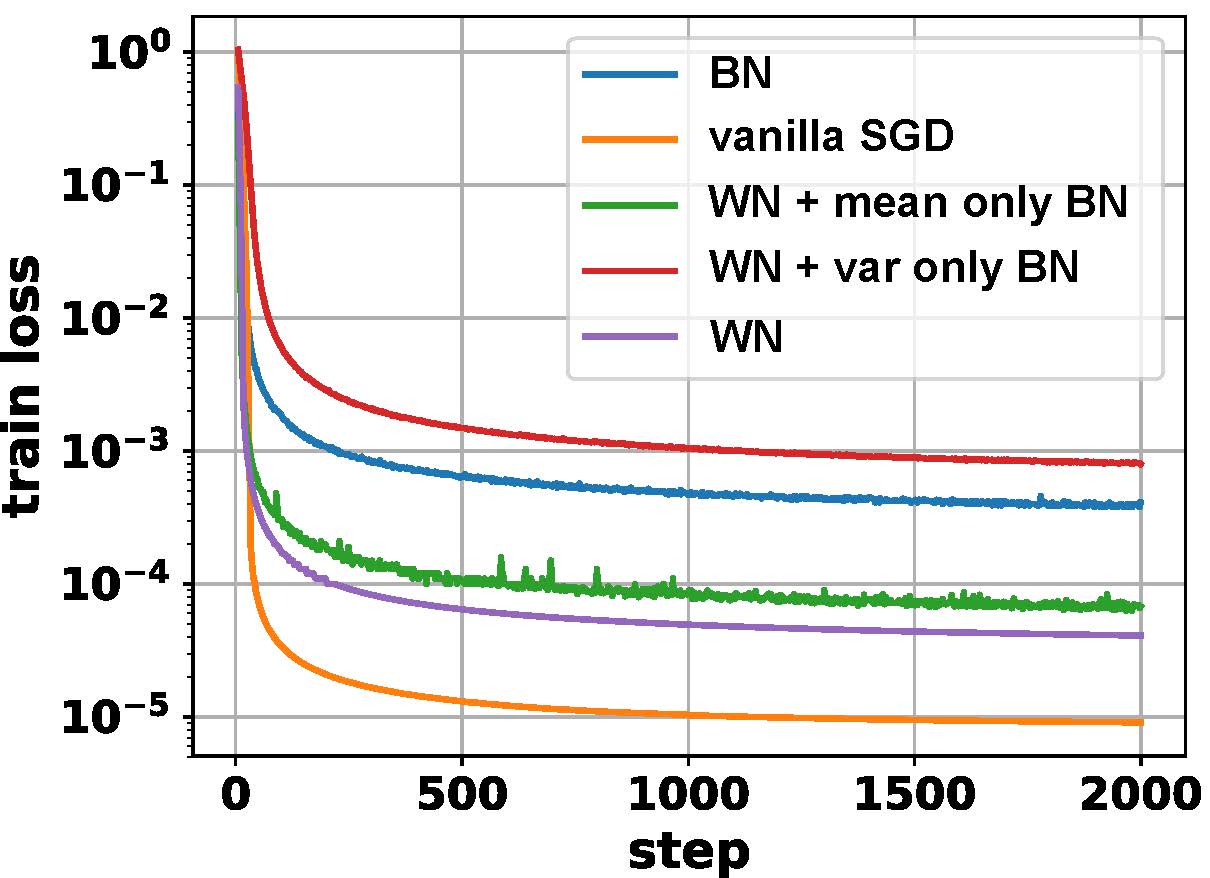
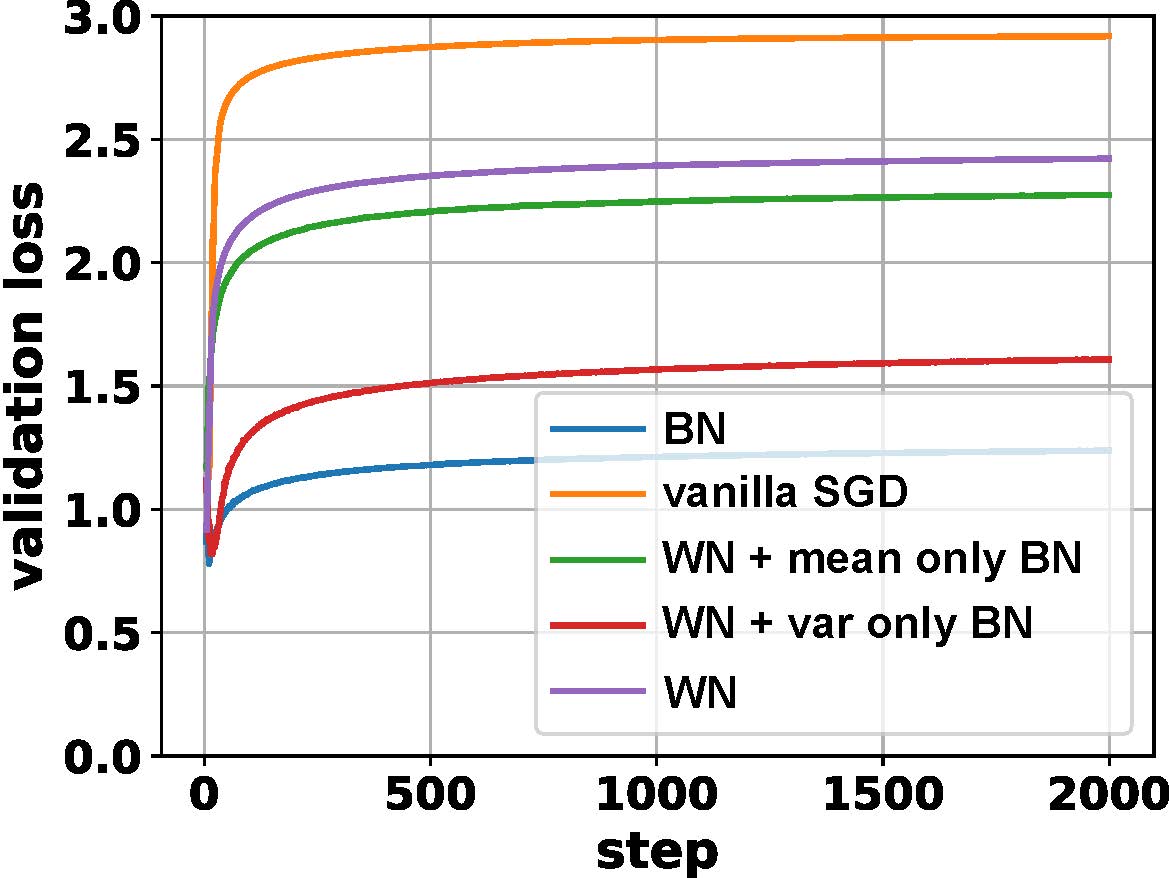
在这里我们比较普通SGD、BN、WN、WN+均值BN，以及WN+方差BN的泛化能力。前三者在前文中有所介绍这里不再赘述。“WN+均值BN”是指维持WN形式不变，但替换 $\mathbf{w}^T\mathbf{x}$ 为 $\mathbf{w}^T\mathbf{x}-\mu_\mathcal{B}$ 以增加WN中由均值噪声所贡献的正则化。同理“WN+方差BN”则替换 $\mathbf{w}^T\mathbf{x}$ 为 $\frac{\mathbf{w}^T\mathbf{x}}{\sigma_\mathcal{B}}$ 以增加WN中由方差噪声所引起的正则化。

下图表示这几种不同归一化方法的泛化误差 (即“validation loss - train loss”)。由图中可见BN对泛化误差的抑制要明显好于其他方法。与此同时“WN+均值BN”与“WN+方差BN”的泛化能力均位于BN与WN之间，说明 $\mu_\mathcal{B}$ 和 $\sigma_\mathcal{B}$ 带来了不同的泛化能力。单独加上其中一项后其正则能力不如BN，实际中往往还需要加入额外的约束。

2.4.3 BN与批量大小

上图是BN对模型泛化误差影响的直观体现。依据本文分析，BN的正则效果是直接作用于每一层的有效缩放量 $\gamma$ 上的。同时我们已有结论：BN的隐含正则能力随着批次大小增加而减小。但是在深层网络里观察到这一点并不容易，主要由于深层网络中会有多个局部最优解，即一个隐含层的网络输出的缩小可以由下一层输出的扩大来弥补。这些问题都使得在深层网络中并不是每一层都符合我们之前在单层网络上推导出来的正则化结论。为了解决这一问题我们从普通SGD出发，将每层的BN逐层打开以观察 $\gamma^2$ 的值以及泛化误差随着批次大小变化的变化。

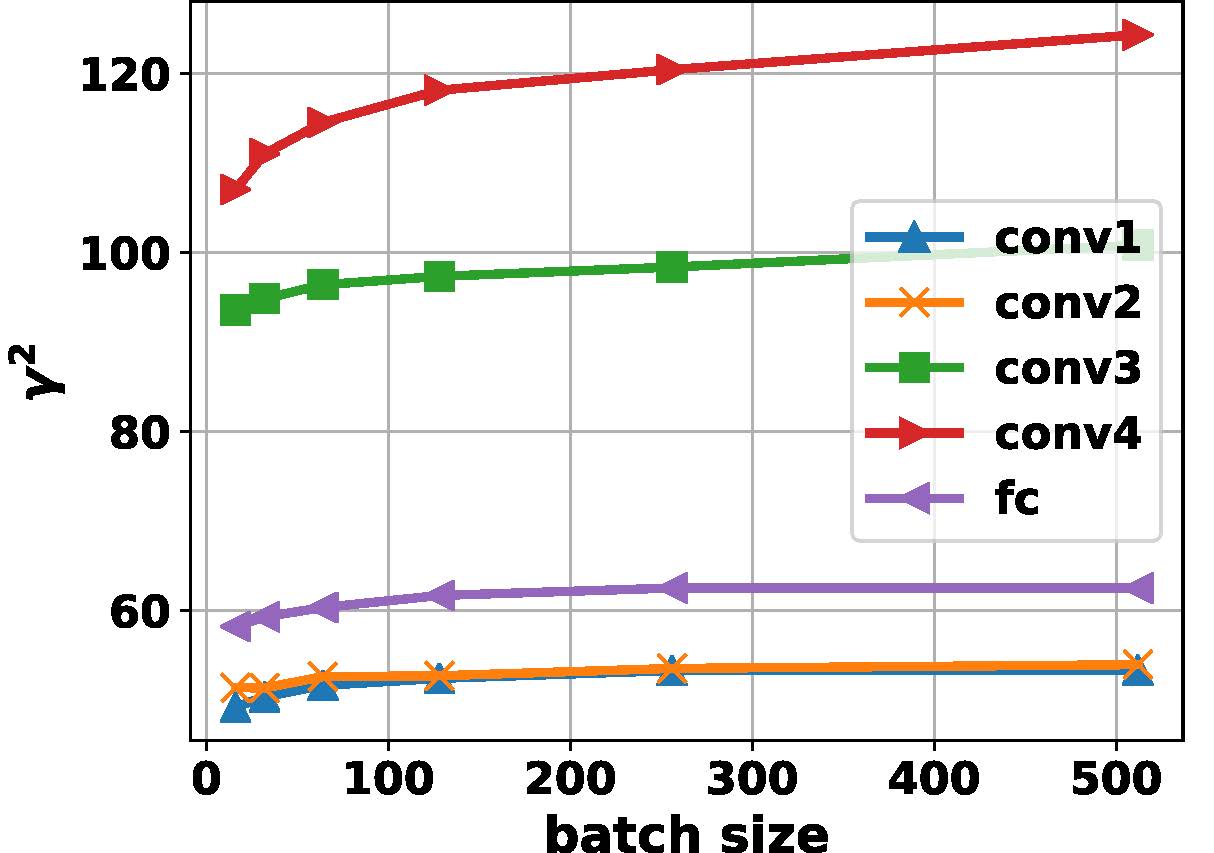
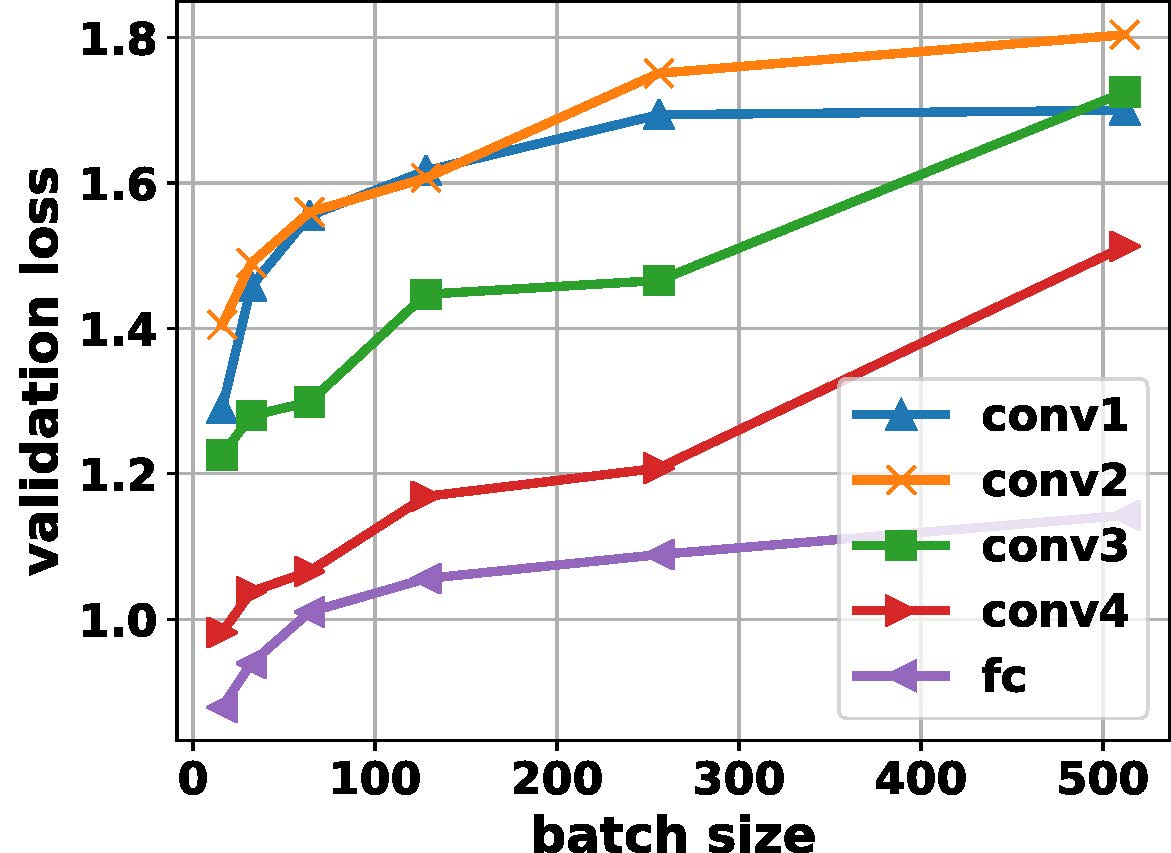
由上图可以看出当某一层BN打开时，该层的 $\gamma^2$ 值随着批次大小增加而增加。这种现象适用于所有层。这是由于批次大小增加而使得BN对 $\gamma$ 的正则效果减弱导致的。同时也可观察到测试误差由于正则的减弱也随着批次大小增加而增加。

2.4.4 BN、WN与Dropout不兼容？

尽管BN网络在小批次训练时给网络带来自适应的Gamma衰减，从而让泛化性能更好。但是BN在批次较大时的表现却不尽人意。根据前文分析，这主要是由于正则项与批次大小成反比，所以大批次时网络的正则能力较弱。一个针对BN的改进是WN，由于BN网络在训练过程中需要不断统计每层的 $\mu_{\mathcal B}$ 和 $\sigma_{\mathcal B}$，会耗费额外的计算资源。相比起来WN在优化过程中只需计算 $\mathbf{w}$ 的模，计算开销会小得多。但是WN因为没有BN所隐含的正则效果而使其在CNN的训练效果大打折扣。综上在大批次的BN网络和WN网络中改进它们的正则能力均有十分重要的意义。

L2正则？：一个直接的想法是在CNN中加入对 $\gamma$ 的正则。实际上这种做法的效果并不好，原因是BN隐含的正则项并不是一个常数而是一个与当前正向与反向参数均有关的值。人工调节很难使得各层均有对应的自适应正则参数，同时引入了复杂的超参系统。这一点在前面也有提到。

BN+Dropout：BN正则项中出现的跟FIM相关的系数与dropout中隐含的正则项类似。因此我们试图采用BN+dropout来额外增加CNN在大批次学习中的正则化强度。下图显示在Cifar-10训练中，若批次由64增加到256时模型的测试误差会显著增加，同时top-1准确率显著降低。但如果在每个BN层后面加入一个dropout层 (ratio=0.125)，这时测试集上的精度甚至会回升到超过原有 $M=64$ 时的准确率。这一现象表面上与BN原文中dropout无法弥补BN效果这一结论有所违背。但实际上，一般而言之前网络训练过程中的批次都较小 ($\sim 32$)，只是在并行计算能力提升之后超大批次的训练才成为可能 (对于Imagenet，批次大小可达60k)。而在小批次训练中BN隐含的正则化能力本身已较强，所以额外dropout引入的正则作用不明显，反而可能带来过大的噪声使得网络无法更好的训练。另外dropout与BN的相对位置也很重要。以往试图利用dropout改善BN的工作将其放在BN之前。但是由于dropout在测试阶段不会带来噪声而BN在测试阶段用的是moving average，导致了网络在测试阶段的统计量有偏差。实际结果也显示dropout放在BN之后效果更好。类似的结论在⁶等的工作中也有提及。

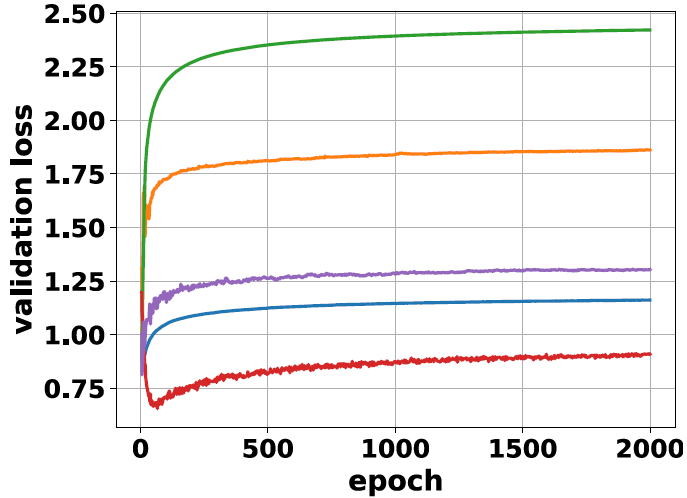
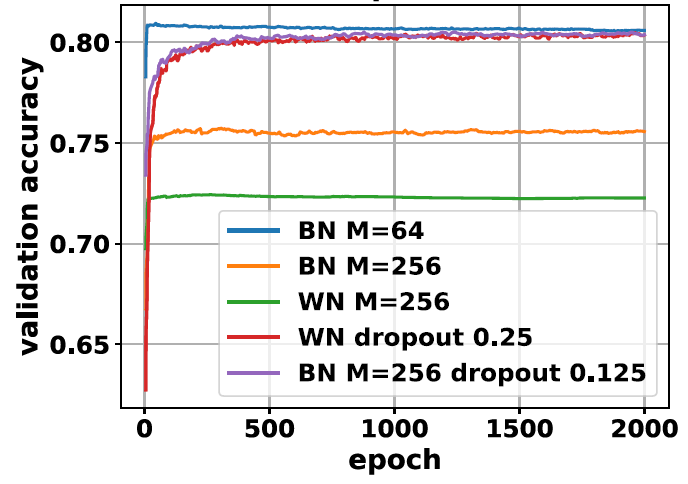
WN+Dropout：因为BN在本文的假设条件下可以认为是WN+ $\gamma$ 正则，所以WN的表现加上dropout后也可能得到提升。如上图所示当WN加上dropout (ratio=0.25) 后其top-1准确率由0.73大幅提升到0.80，甚至与BN $M=64$ 训练的结果可相比。因此加入dropout后WN引入了额外的正则化系数使得其具有更好的泛化性能。